One of the simplest and yet most important questions in astronomy relates to how far away the objects we study are. This question is relevant to all astronomical objects, from stars to galaxies and beyond. It's important to understand how far away these objects are because that's how we know how large or how luminous they are, and knowing these characteristics is necessary to build up our model of the Universe.
Despite this, measuring distances in astronomy is incredibly difficult, because sometimes all that can be resolved about an object is a single dot of light. For this reason astronomers have built up a series of methods for estimating the distances to objects, each of which is used for different types of object at different distances, and with each method calibrated using one of the other methods. We refer to this as the distance ladder.
The most fundamental method to determine distance, and the most important step on the distance ladder, is known as parallax. Parallax is the effect by which objects at different distances change their apparent position based on your vantage point.
In astronomy this is possible because the Earth changes it's position throughout the year as it orbits the Sun. Because of this the apparent positions of stars relative to each other change throughout the year.
This diagram shows an example of this. When the Earth is on the opposite side of the Sun the line of sight to a nearby star will change relative to more distant stars. The apparent shift in the position of the nearby star is known as the parallax angle and is directly related to the distance to the star - the nearer the star is, the larger the parallax angle will be.
You can simulate a small-scale version of this process for yourself using your two eyes as the two different vantage points. Hold out your hand in front of your face with a single finger pointing vertically upwards. Close one eye and look at the scene in front of you. Then switch the eye that is closed and see how the scene in front of you changes. You should see that the position of your finger changes relative to the background scene it is projected against.
In this example your finger is the nearby star and the background scene is the background stars. If you try moving your finger closer or further away from your face you should see that the apparent shift in your finger's position when you switch your closed eye changes - does the shift get larger when your finger is closer or further away from you?
Because parallax is such an important method of distance determination it has led to the most commonly used unit of distance in astronomy, the parsec. A parsec (1 pc) is the distance at which an object's apparent position shifts by 1 second of arc (1/3600 of a degree) as the Earth orbits the Sun. It's a very small shift, but then a parsec is a very large distance - approximately 30,000,000,000,000 km!
Despite how big the parsec is, all the stars in the sky are actually more distant than a parsec, and many are much much further than this. Because of this astronomers need very precise instruments and telescopes to be able to measure the tiny changes that result from the parallax effect. One of the most famous such telescopes was the Hipparcos space telescope, which measured parallaxes for thousands of stars out to distances of several hundred parsecs. The Hipparcos telescope was one of the most important telescopes in astrophysics, simply because of the unprecedented accuracy with which it measured the distance to so many stars. The successor to Hipparcos, the Gaia space telescope, was launched about a year ago, and is continuing this mission as we speak.
For very distant objects where the parallax method is not feasible the only way to determine distances is to estimate how intrinsically bright the object is and then determine its distance based on how bright it appears to us. To do this we need to use objects with a known, or predictable, brightness, often referred to as standard candles. Examples of this including pulsating stars such as Cepheid variables, which Edwin Hubble used to determine distances to other galaxies. This method is most commonly applied to distant galaxies that are too far away to use parallax, but close enough to resolve and study their individual stars.
Despite this, measuring distances in astronomy is incredibly difficult, because sometimes all that can be resolved about an object is a single dot of light. For this reason astronomers have built up a series of methods for estimating the distances to objects, each of which is used for different types of object at different distances, and with each method calibrated using one of the other methods. We refer to this as the distance ladder.
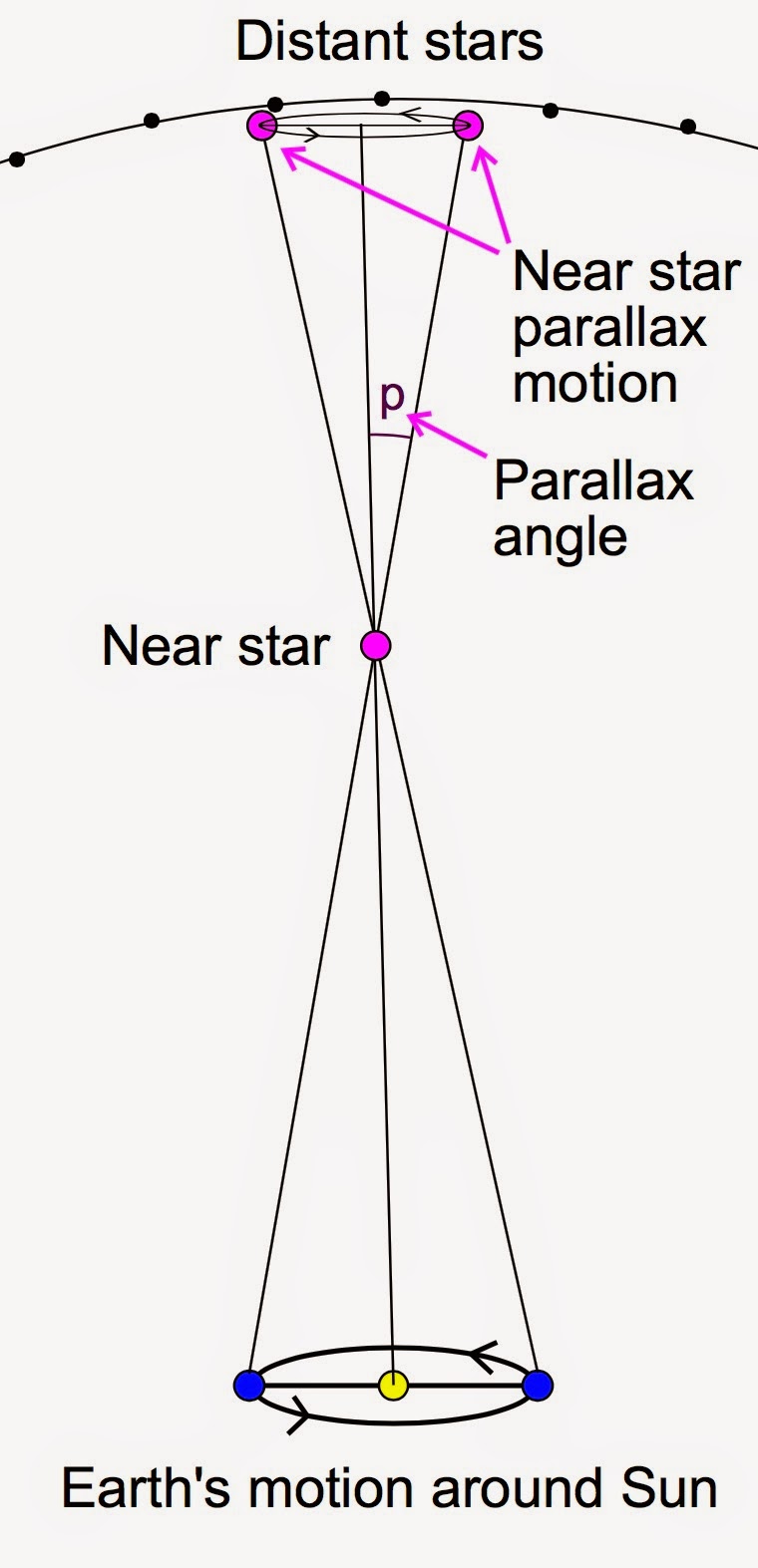 |
| The Parallax Effect (Credit: Wikipedia) |
This diagram shows an example of this. When the Earth is on the opposite side of the Sun the line of sight to a nearby star will change relative to more distant stars. The apparent shift in the position of the nearby star is known as the parallax angle and is directly related to the distance to the star - the nearer the star is, the larger the parallax angle will be.
You can simulate a small-scale version of this process for yourself using your two eyes as the two different vantage points. Hold out your hand in front of your face with a single finger pointing vertically upwards. Close one eye and look at the scene in front of you. Then switch the eye that is closed and see how the scene in front of you changes. You should see that the position of your finger changes relative to the background scene it is projected against.
In this example your finger is the nearby star and the background scene is the background stars. If you try moving your finger closer or further away from your face you should see that the apparent shift in your finger's position when you switch your closed eye changes - does the shift get larger when your finger is closer or further away from you?
Because parallax is such an important method of distance determination it has led to the most commonly used unit of distance in astronomy, the parsec. A parsec (1 pc) is the distance at which an object's apparent position shifts by 1 second of arc (1/3600 of a degree) as the Earth orbits the Sun. It's a very small shift, but then a parsec is a very large distance - approximately 30,000,000,000,000 km!
Despite how big the parsec is, all the stars in the sky are actually more distant than a parsec, and many are much much further than this. Because of this astronomers need very precise instruments and telescopes to be able to measure the tiny changes that result from the parallax effect. One of the most famous such telescopes was the Hipparcos space telescope, which measured parallaxes for thousands of stars out to distances of several hundred parsecs. The Hipparcos telescope was one of the most important telescopes in astrophysics, simply because of the unprecedented accuracy with which it measured the distance to so many stars. The successor to Hipparcos, the Gaia space telescope, was launched about a year ago, and is continuing this mission as we speak.
 |
| The European Space Agency's Hipparcos satellite (Credit: CNES) |
For very distant objects where the parallax method is not feasible the only way to determine distances is to estimate how intrinsically bright the object is and then determine its distance based on how bright it appears to us. To do this we need to use objects with a known, or predictable, brightness, often referred to as standard candles. Examples of this including pulsating stars such as Cepheid variables, which Edwin Hubble used to determine distances to other galaxies. This method is most commonly applied to distant galaxies that are too far away to use parallax, but close enough to resolve and study their individual stars.
No comments:
Post a Comment